Algorithms

• 1: Differential gene expression (DEG) analysis
• 2: Dimensionality reduction methods
• 3: Enrichment analysis
• 4: Exploratory analysis
• 5: Mapping between peptidomics and/or proteomics features

1 - Differential gene expression (DEG) analysis

Purpose of DEG analysis

DEG analysis aims to identify features (e.g. genes, proteins) with altered expression levels across different experimental conditions or sample groups, providing valuable insights into biological processes affected by specific contexts (e.g. disease, treatment, or developmental stage).

DEG methods in PanHunter

DESeq2 and limma are available in PanHunter. They are two go-to tools for researchers studying feature expression patterns and regulatory mechanisms. Their robustness, accuracy, and widespread adoption make them valuable assets in the field of bioinformatics.

DESeq2

How does DESeq2 work?

DESeq2 operates through the following steps:

• Data Preparation: DESeq2 takes raw count data and models them using a negative binomial distribution. The data are then normalized to account for differences in sequencing depth and library size using the median-of-ratios method.

• Variance Stabilization: DESeq2 stabilizes the estimated dispersion of individual feature expression by sharing information between the features with similar expression levels. The strength of the stabilization is influenced by both the global and individual variance estimated by the Empirical Bayes method.

• Statistical Models: DESeq2 employs generalized linear models to account for multiple factors (e.g. batch effects) influencing expression profiles.

• Differential Expression Testing: DESeq2 compares feature expression levels between conditions (e.g. treatment vs. control) and identifies features that show significant differences. Wald tests are used to test for significance.

• Results: DESeq2 provides lists of differentially expressed features along with statistical significance (adjusted p-values) for robust downstream interpretation.

For more information, see the detailed documentation - DESeq2: Differential gene expression analysis based on the negative binomial distribution.

limma

How does limma work?

limma (Linear Models for Microarray Data) is a versatile tool initially designed for analyzing gene expression data from microarrays. However, it has found utility beyond microarrays in other high-throughput sequencing data analyses. Here’s how it operates:

• Normalization: Limma takes log-norm transformed expression data as input, assuming a normal distribution. Raw counts can also be submitted to limma via the VOOM transformation.

• Variance Stabilization: Limma uses the mutual information of the feature expressions to moderate the residual variances. This means that the estimated variation of a single feature is stabilized to the global feature variance.

• Statistical Models: It employs feature-wise linear models to account for multiple factors. This allows differential analysis across multiple contrast levels.

• Differential Expression Testing: Limma compares feature expression levels between conditions (e.g. treatment vs. control) and identifies features that show significant differences. Moderate t-statistics, adjusted for multiple testing, are used to estimate the significance of differential expression analysis results.

• Results: Limma provides lists of differentially expressed features along with statistical significance for robust interpretation. Estimated standard errors can also be extracted from the results of limma analyses.

For more information, see the detailed documentation - limma.

How does PanHunter calculate standard error (SE)?

Since the standard error (SE) is not directly given by the limma tool, PanHunter generates a matrix containing the standard errors for each coefficient and feature as suggested by Gordon Smyth. For more information, see this discussion - Standard error and effect size from Limma.

How to choose between DESeq2 and limma for DEG analysis?

DESeq2 is robust for small sample sizes and is designed for count-based data only (e.g. RNA-Seq data). Limma takes continuous numbers and is therefore applicable to proteomics data. Limma consumes fewer computational resources and may be a better option for large transcriptomics data.

In PanHunter, DESeq2 is selected by default for transcriptomics data, and limma for proteomics and microarray data. The DEG analysis method can be customized in the New Comparison app according to scientific needs.

2 - Dimensionality reduction methods

What is dimension reduction?

Dimension reduction is a tool that enables visualization of high-dimensional omics data in 2D. The main goal of any dimension reduction method is to extract the most important information from the data, usually by analyzing the way samples are clustered.

If two points (samples) are close in the 2D representation, they are also similar in high-dimensional space, e.g. they have a similar transcriptome or proteome profile.

Dimensionality reduction methods available in PanHunter

The algorithms for dimensionality reduction available in PanHunter are:

• PCA – Principal component analysis. A linear deterministic dimensionality reduction method. For more information watch this 5-minute explanation and detailed video tutorial or read this article.

• UMAP - Uniform manifold approximation and projection. A non-linear stochastic dimensionality reduction method. UMAP has two hyperparameters - number of neighbors and minimum distance - that can be set within PanHunter. The number of neighbors balances the local and global structure in the data. Low values result in a focus on very local structure, while high values focus on global structure. The minimum distance influences the degree of separation between clusters by controlling the compactness of points in the embedding space. In addition, it is also possible to set the seed, which ensures reproducibility by setting the starting point for the random number generator. Check out this video tutorial or read the article for more explanations.

• t-SNE – t-distributed stochastic neighbor embedding. A nonlinear stochastic dimensionality reduction method. t-SNE has a hyperparameter, perplexity, that can be adjusted in PanHunter. The perplexity parameter, as highlighted by L. van der Maaten & G. Hinton (2008), serves as a critical measure to determine the appropriate number of neighbors. This measure, with typical values ranging between 5 and 50, provides a nuanced approach to evaluate the local structure of the data. In addition to the perplexity parameter, it is also possible to set the seed, which ensures reproducibility by setting the starting point for the random number generator. Check out this video explanation or read this article for more explanations.

• PHATE – Potential of heat-diffusion for affinity-based trajectory embedding. A nonlinear stochastic dimensionality reduction method which preserves both global and local structures. It is used with the default parameters set in scanpy. For more information see this article or learn more on here.

📝 Setting seeds: Users are encouraged to try multiple random seeds to validate consistency and robustness of observed pattern within the resulting 2D space.

For more information on comparison between PCA, UMAP and t-SNE methods, and which one to use, check out following resources:

• Dimensionality Reduction: PCA, t-SNE, and UMAP
• Latent Space Visualisation: PCA, t-SNE, UMAP | Deep Learning Animated

3 - Enrichment analysis

What is enrichment analysis?

Gene set enrichment analysis (GSEA) is a computational method used to evaluate the associations of a list of differentially expressed genes to a collection of pre-defined gene sets, where each gene set has a specific biological meaning. Once differentially expressed genes are significantly enriched in a gene set, the conclusion is made that the corresponding biological meaning (e.g. a biological process or a pathway) is significantly affected.

Enrichment Analysis helps uncover biologically relevant patterns in large-scale omics data, providing insights into the collective behaviour of functionally related genes, revealing potential biological processes associated with the observed changes in gene expression.

Enrichment Analysis methods need a statistical test to determine whether the predefined gene sets are statistically enriched. As input, enrichment analysis methods usually require either a list of significant differentially expressed genes and predefined gene sets, which can be obtained from various sources such as pathway databases, or curated collections of genes associated with specific functions. An overview of methods and input data used in PanHunter is explained below.

Enrichment analysis in PanHunter

Enrichment analyses in PanHunter are performed during comparison calculation. After differential expression analysis is performed and the newly generated comparison is successfully saved in PanHunter, post-processing steps are automatically performed. The full list of all post-processing steps can be found here. Gene ontology (GO) and pathway enrichment are performed among those. Additionaly, enrichment analysis can be performed in the Enrichment visualization app.

Algorithms and methods used for enrichment in PanHunter are detailed below.

Comparison post-processing

       Gene Ontology (GO) Enrichment

The GO term enrichment in PanHunter utilizes evoGO package, developed by Evotec International GmbH, in conjunction with the weight algorithm. The evoGo algorithm with weight option performs down weighting of genes attributed to a term in all its ancestor terms in case the term is more significant that the corresponding ancestor. This approach decreases redundancy in the resulting list of significantly enriched terms. Full documentation on evoGO package is available here.

Correction for multiple testing are performed with Benjamini-Hochberg method (described here) resulting in reported FDRs.

For the calculation, PanHunter uses the following input data:

• The latest version of Gene Ontology from GO Consortium website and GO term annotation from Ensembl database
• List of features generated by differential expression analysis and reported in the comparison

The results of post-processing analyses for specific comparison can be found and explored in the TopTables app, as described here.

       Pathway Enrichment

The pathway enrichment analysis uses Fisher’s test, Wilcoxon test and Kolmogorow-Smirnow test to perform analysis. P-values as well as p-values adjusted for multiple testing in form of FDR are reported. Benjamini-Hochberg methodology is used for adjustment.

For the calculation, PanHunter uses the following input data:

• The latest version of human pathways from Wikipathways, an open platform and database for creating, curating, and sharing biological pathways.
• List of features generated by differential expression analysis and reported in the comparison.

The results of post-processing analyses for specific comparison can be found and explored in the TopTables app.

What is the difference between Fisher’s test, Wilcoxon test and Kolmogorow-Smirnow test?

The Fisher test is used for dichotomous variables and is suitable for smaller sample sizes.

The Wilcoxon test and the Kolmogorov-Smirnov (KS) test are used for continuous or ordinal data. The main difference between them is that the Wilcoxon test is more sensitive to differences in location of the distributions (such as median or mean), while the KS test is more sensitive to differences in shape of the distributions (such as variance or skewness).

Furthermore, Fisher’s test assesses the overrepresentation of a specific pathway based on the number of significantly regulated features, whereas Wilcoxon and KS test do the assessment on the logFC level.

Enrichment Visualization App

Although enrichment analysis is performed together with post processing steps during the comparison calculation, a dedicated Enrichment Visualization App provides user with additional options to customize and visualize gene set enrichment analysis outputs. To learn more about usage of the app, have a look at detailed documentation on the Enrichment Visualization App available here.

Enrichment with specified gene set collections is performed by Fisher’s test reporting p-values, with the exception being the GO term enrichment analysis which uses evoGo package in combination with Weight method, as described here (link).

Additionally, the Bonferroni correction reporting the family-wise error rate (FWER) and Benjamini-Hochberg and Benjamini-Yekutieli methods reporting false discovery rates (FDRs) are performed.

The output of the enrichment analysis and different visualization options available within this app are described in the app documentation.

4 - Exploratory analysis

What is exploratory analysis?

The goal of exploratory analysis is to determine which of the associated metadata best explains the clustering of the abundance data. Exploratory analysis in PanHunter can be performed in the New Comparison app on categorical and numerical values, or feature abundances.

How is exploratory analysis done in PanHunter?

The calculation is done in the following way:

1. First, a distance matrix between samples is computed using the metric that was selected for dimension reduction (default is Euclidean).

2. Second, p-values are calculated with different statistical tests depending on the metadata used for the exploratory analysis:

For categorical variables Mann-Whitney test is employed two times.

• First time to check if the distances between the samples that share a level of the analyzed category are smaller than the distances between samples that fall into different level of this category. Thus, it is tested if this category drives the sample clustering. For example, we are analyzing the category sex that has the three levels ‘Male’, ‘Female’ and ‘Unknow’. It is tested whether the distribution of the pairwise distances between all ‘Male’, all ‘Female’ and all ‘Unknow samples is smaller than the distribution of pairwise distances between ‘Male’ and ‘Female’, ‘Male’ and ‘Unknown’ and ‘Female’ and ‘Unknown’ combinations.
• Second time the Mann-Whitney test is employed is to check, whether the distances between the samples for a particular level of a category are smaller than the distances between all the samples. Thus, it is tested whether this level of the category drives the samples clustering. For example, we are analyzing again the category sex that has the three levels ‘Male’, ‘Female’ and ‘Unknow’. Now it is tested if ‘Male’ is driving the clustering by testing if the distribution of the pairwise distances between all ‘Male’ samples is smaller than the distribution of pairwise distances between ‘Male’ and ‘Female’, ‘Female’ and ‘Female’, ‘Male’ and ‘Unknown’, ‘Female’ and ‘Unknown’ and ‘Unknown’ and ‘Unknown’ combinations.

For numerical variables and features, Spearman’s rank correlation (ρ) is calculated between the distances for the samples and the Manhattan distances between the values of the variable that is being analyzed. The p-value for the null-hypothesis that ρ = 0 and the alternative that ρ > 0 is computed via asymptotic t approximation.

3. As a last step, a statistical score (StatScore) is calculated for each variable, which is equal to the -log10 transformation of the p-value, capped at 100. For numerical variables and features, the correlation is reported along in addition to StatScore.

5 - Mapping between peptidomics and/or proteomics features

Since PanHunter is a true multi-omics platform, the challenge arises to match features or information from different entities. Especially for proteomics and peptidomics data this is of high relevance, as the measured intensities usually cannot be associated to a single protein, but only to a group of possible proteins. Such groups may only contain isoforms of the same canonical protein, but they can also contain completely independent proteins. Comparing the measurements of such protein groups (PGs) across different datasets is a common task in the data analysis.

IDs for proteins and peptide/PTMs

The whole procedure of mapping features between entities relies on well-defined IDs, that uniquely identify a feature. This can be for example the ID used from the “ensembl” database or from the ncbi database. For the identification of proteins, PanHunter uses the Uniprot ID. Protein groups on the other hand are then simply a list of such Uniprot IDs.

Peptides are not part of any of these databases, so PanHunter allows to use arbitrary IDs. The only requirement for them is that they are unique within a study. During the preprocessing the used software DiaNN, Maxquant or Spectronaut is identifying from which protein a peptide is coming from. Hence, each peptide gets associated to a protein group of possible proteins. In this process, also post-translational modifications (PTMs) are identified and the position and the type of the modified amino acid is retrieved. As the ID can be arbitrary, it is not guaranteed that it is valid across different studies. Hence, for this purpose PanHunter creates an internal ID. Currently, this internal ID consists out of the associated protein group, the modified amino acid and the location, but this might change in the future. Uniqueness is not a strict requirement for the internal ID, even if the probability for it is very high.

Mapping algorithms

As stated above, it is often required to match features from different entities. So, one dimension of the used algorithms are the types of the involved features, e.g a PTM/PTM, a PTM/PG or a PG/PG match. Apart from that, there are two algorithms per type available, namely the “exact matching” and an “explosion matching”. The details and the use-cases are explained below. Additionally, the workflows are also visualized by graphs. There, the columns used for a merge are colored in the same way. The FDR column is used here, as a placeholder for all additional columns that might be present.

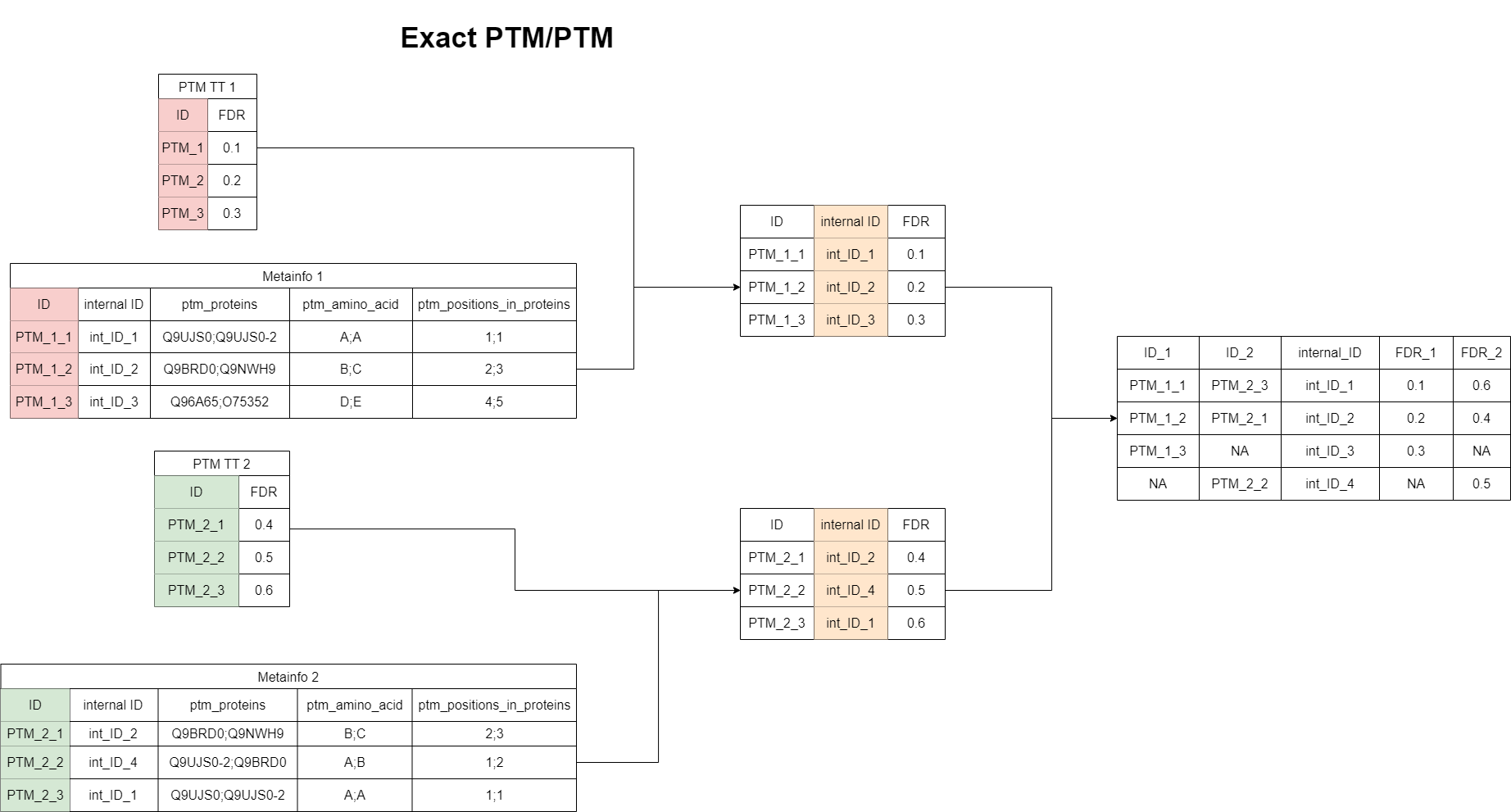
“Exact matching” for the PTM/PTM case

This case is the most simple one, as it is done based on the internal ID. Two PTM features are matched, if their internal IDs are fully identical. This means the same PG has been associated to them and all modifications are also identical. No isoform removal or any other modification of the associated protein groups are applied here. Therefore, this algorithms is quite strict, but the results are reliable in a sense, that the matched features are exactly identical in both datasets.

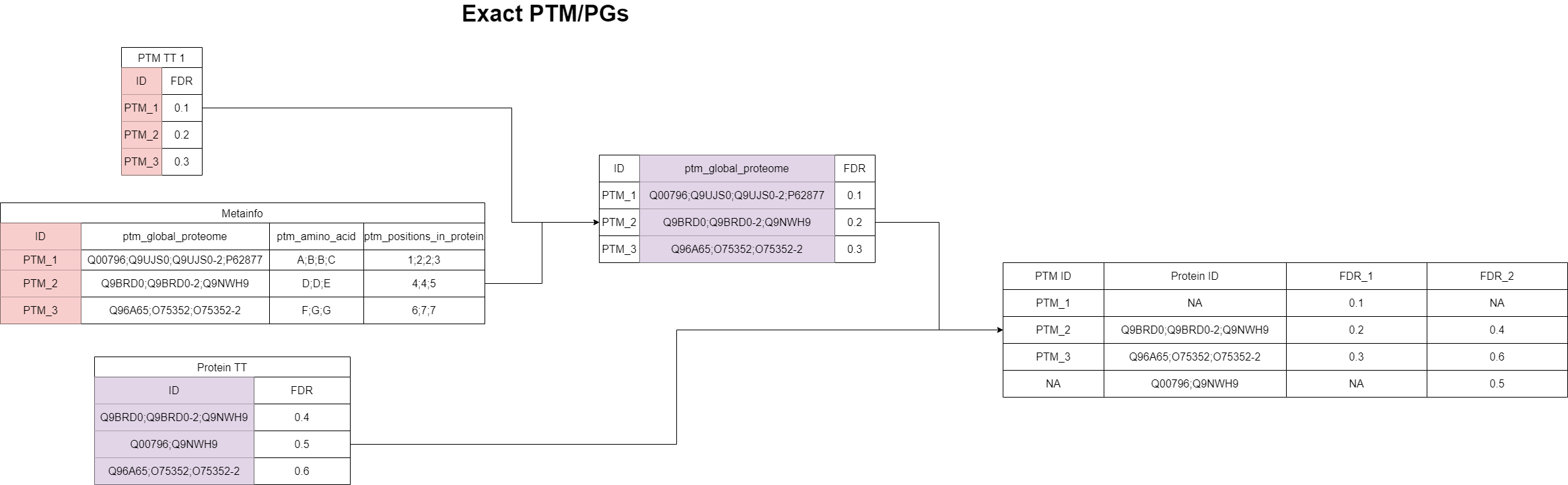
“Exact matching” for the PTM/PG case

Here, we are dealing with PTM data on the one hand and proteomics data on the the other. As before, the intention of this “exact matching” is having a high confidence when finding a match. This is not given for two unrelated peptidomics/proteomics studies, because the features were potentially identified under completely different circumstances. Hence, for doing this matching, it is required that the studies are indeed related to each other. This information can be stored in the sample table during data integration.

If the studies are related, PanHunter doesn’t use the protein groups that were identified by DiaNN, Spectronaut or Maxquant as PTM associated protein groups but instead each PTM feature is mapped using an proprietary mapping algorithm to a protein group in the proteomics dataset during data integration. These specifically inferred protein groups will then be used for mapping to the related proteomics dataset, and again, the protein groups must be fully identical to be considered a match. This also means that no isoform removal or any other modification on the protein groups are made in this process.

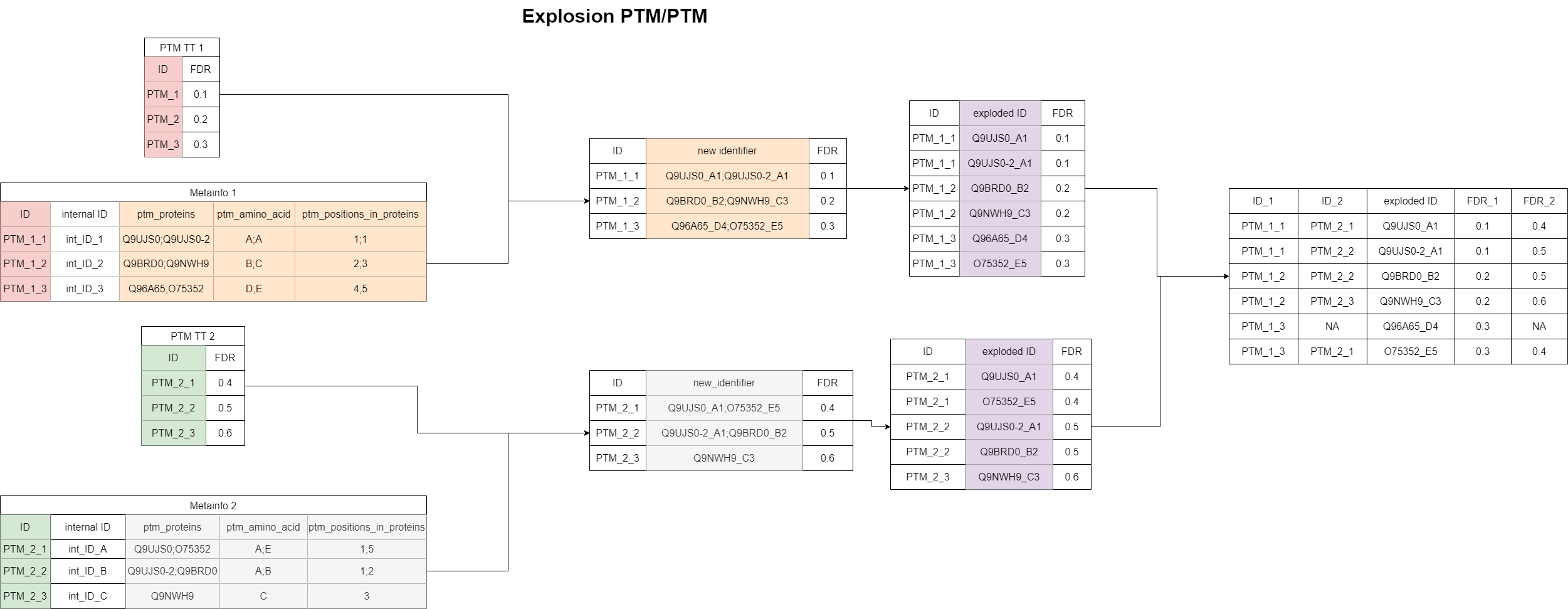
“Explosion matching” for the PTM/PTM case

Compared to the “Exact matching”, the “Explosion matching” is less strict and more matches will be found. In this context, “explosion” means that the list of associated proteins gets split-up to single proteins. Each protein now gets appended by the modified amino acid and the location of the modification. Furthermore, in case of multiple modifications, the protein is appended by each modified amino acid and location separately (e.g., Q9UPW0_K_K_40_41 results in Q9UPW0_K_40 and Q9UPW0_K_41). Two PTM features are now considered as a match, if any of these protein features are identical between them. If the overlap is larger than just one feature, the list of matched features is made unique, because the information would be redundant. This will be explained in the apps in more details. This algorithm can result in multimappers, if a PTM is part of multiple protein groups. Within this algorithm, isoforms are cleaned, such that different isoforms are considered as a match.

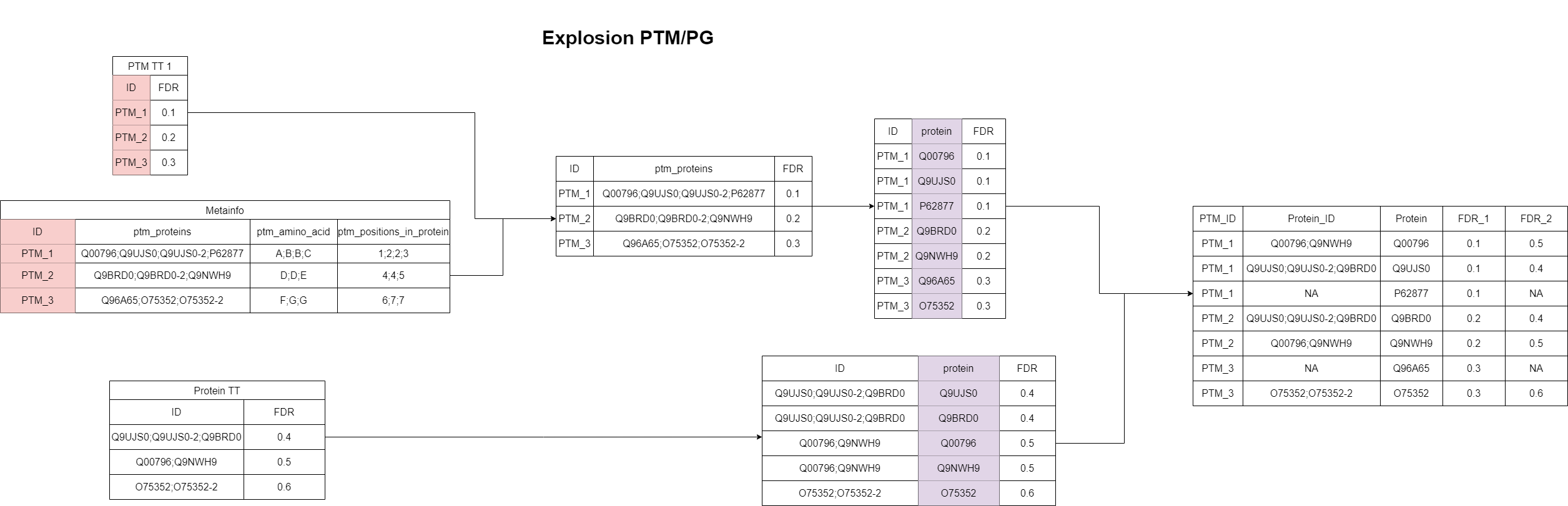
“Explosion matching” for the PTM/PG case

Since the “Explosion” algorithms are less strict, we don’t require any relations between the datasets as for the “Exact matching” algorithm for the PTM/PG case. Here again, the associated protein groups for the peptidomics study and the protein groups of the proteomics study are both split up (“exploded”). Differently than for the PTM/PTM case, here isoforms are converted to the canonical forms for both datasets. A PTM feature matches to a proteomics feature, if any of the “exploded” proteins is found in the other dataset. Again, this can result in multimappers as all PTMs of a canonical protein will match to all protein groups containing this protein.

“Explosion matching” for the PG/PG case

For the matching between two proteomics studies, always the “Explosion matching” is used. Again, for both datasets the protein groups get “exploded”. Two features match, if any single protein is found in both protein groups. Isoforms are converted to the canonical form here as well.